Wie lang muss eine Garage sein
Wie lang muss eine Garage sein?
von Benno Grabinger
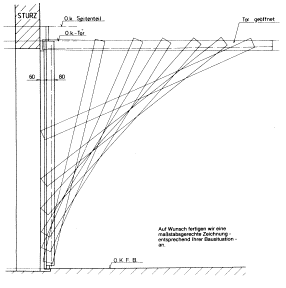
Mathematik kommt vor!
Die Astroide, eine ästhetisch ansprechende Kurve, lässt sich bei der Bewegung eines Garagentores oder der Schwingtoren zu Geräteräume von Turnhallen „wiederentdecken“. Dabei werden unterschiedliche Phasen der Mathematisierung dargestellt in denen der Computer eine entscheidende Rolle als Zeichengerät und als Werkzeug für umfangreiche Termumformungen spielt. Geometrische Kenntnisse und Paramerterdarstellungen von Kurven sowie die Methoden der Differentialrechnung werden in interessanten Zusammenhängen angewandt.
Artikel-Datei: 
Garage.pdf (270 K)
Fadenbilder analysieren mit Derive - Hüllkurven
von Michael Bostelmann
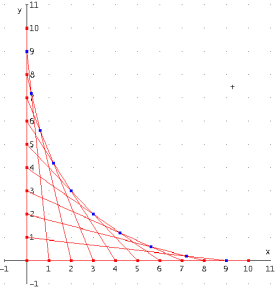
Fadenbilder sind immer wieder faszinierende geometrische Objekte. Sie lassen sich mit einfachen Hilfsmitteln erstellen und bieten vielfältige Anreize zu interessanten mathematischen Fragestellungen im Gebiet der Hüllkurven.
Mit Derive lassen sich Fadenbilder ebenfalls konstruieren, wobei die zugrunde liegenden mathematischen Zusammenhänge in den verwendeten Konstruktionsvorschriften sichtbar werden. Daran knüpfen verschiedene Untersuchungen zu Hüllkurven an.
Artikel-Datei: Fadenbilder.pdf (290 K)
