Drei Kandidaten werden ins Studio geleitet. Sowie einer von ihnen den Raum betritt, setzt die hübsche Assistentin des Quizmasters ihm einen Hut auf den Kopf, und zwar einen blauen oder einen roten, je nachdem, wie eine zuvor geworfene Münze fällt.
Der Kandidat kann seinen Hut nicht sehen. Nun stehen sie alle drei im Saal, und der Quizmaster sagt: ”Schauen Sie sich die Hüte lhrer Mitspieler genau an und raten Sie dann, welche Farbe lhr eigener Hut hat. Sie dürfen sich nicht mit lhren Mitspielern verständigen, und Sie hören auch deren Antworten nicht.”
Nur eine von zwei Antworten ist richtig, und ich habe keine Ahnung, welche. Kann ich meine Erfolgschance auf mehr als 50 Prozent verbessern?
Artikel-Archiv:  hutproblem.zip (186K)
hutproblem.zip (186K)
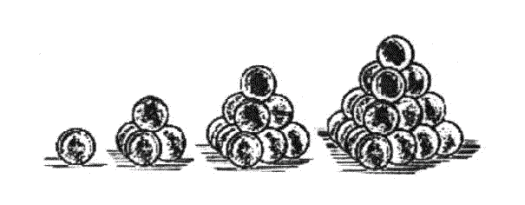
 Die Tennispyramide
Die Tennispyramide Fibonaccis Kaninchen
Fibonaccis Kaninchen Das Benford-Gesetz
Das Benford-Gesetz Das Hutproblem
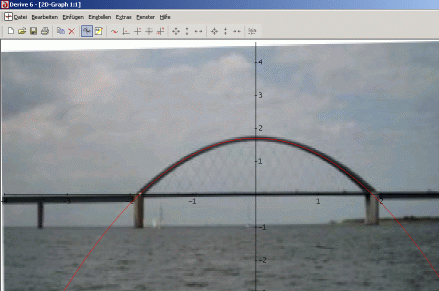
Das Hutproblem Hintergrundbilder auf der 2D-Seite von Derive
Hintergrundbilder auf der 2D-Seite von Derive