Bildungsserver > Mathematik > Sekundarstufe II > MatheAG SII > Materialien für Computer und CAS > Materialien und Sequenzen zum Modell...
Fahrzeugdurchsatz im Kolonnenverkehr- Vergleich von Höchstleistungen im Sport
- Lebenslauf einer Pfandflasche
- Trainingsprogramm für Kugelstoßer
- Eurotunnel
- Vom Modell zur Diffentialgleichung
- Ein Verkehrsproblem
Auch wenn die Materialien bereits einige Jahre alt sind, sind sie nach wie vor aktuell und können leicht an die heute üblichen Medien angepasst werden.
Einleitung
von Gregor Noll und Günter Schmidt
Allgemeine Überlegungen zu Unterrichtssequenzen bei denen Mathematik in Anwendungssituationen entwickelt und zur Problemlösung herangezogen wird.
Artikel-Datei: 
Modellbilden.pdf (9 K)
Fahrzeugdurchsatz im Kolonnenverkehr
von Günter Schmidt
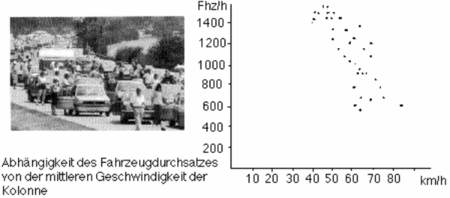
Wie kann man im einspurigen, dichten Kolonnenverkehr einen möglichst großen Fahrzeugdurchsatz erreichen? Der Einfluss verschiedener Parameter wird mit Hilfe von Funktionen, Graphen und Tabellen und deren Bearbeitung mit dem Computer ohne Kalkül der Differentialrechnung untersucht.
Artikel-Datei: Fahrzeugdurchsatz.pdf (201 K)
Vergleich von Höchstleistungen im Sport
von Günter Schmidt
Am Beispiel von Weltrekordzeiten wird aus den Daten ein empirisches Modell entwickelt. Die Gegenüberstellung der Modelldaten mit den gegebenen Realdaten erlauben einen gewissen Vergleich der Leistungen. In Streudiagrammen werden die gegebenen Daten explorativ analysiert und Funktionsgraphen an sie angepasst. Dabei lassen sich Möglichkeiten und Grenzen des mathematischen Modellierens diskutieren. Als Werkzeug wird ein graphischer Taschenrechner eingesetzt. Ähnliche Bearbeitungen sind mit Derive, einer Tabellenkalkulation oder statistischer Software möglich.
Artikel-Datei: Sport.pdf (69 K)
Lebenslauf einer Pfandflasche
von Benno Grabinger
Wie oft wird eine Pfandflasche durchschnittlich wiederverwendet? Welcher Zusammenhang besteht zwischen der Rückgabewahrscheinlichkeit und der Lebensdauer? Diese Fragen werden in einem einfachen Modell zunächst durch Simulation mit dem Computer und Derive beantwortet. Die dabei gewonnenen Erkenntnisse führen schließlich zu einer Modellierung mit der geometrischen Verteilung. Die aus dem Modell gewonnen Ergebnisse werden mit konkreten Angaben aus der Getränkeindustrie verglichen. In einem Anhang werden Informationen und Materialien über die Erzeugung von Zufallszahlen mit Derive als Hintergrundwissen zusammengestellt.
Artikel-Datei: Pfandflasche.pdf (298 K)
Trainingsprogramm für Kugelstoßer
von Ariane Keil
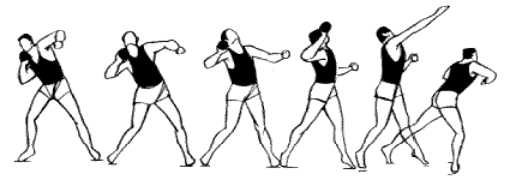
Welche Fähigkeiten sollte man trainieren, um eine möglichst große Leistungssteigerung zu erzielen? Gibt es einen optimalen Abstoßwinkel, welchen Effekt hat die Steigerung der Abstoßgeschwindigkeit? Solche Fragen lassen sich in einem geeigneten mathematischen Modell mit quadratischen Funktionen durch Variation der Parameter untersuchen. Experimentell gewonnene Hypothesen können graphisch verdeutlicht und rechnerisch nachgeprüft werden. Dabei werden dann auch ungewohnte funktionale Abhängigkeiten, etwa die der Stoßweite als Funktion des Abstoßwinkels graphisch dargestellt und analysiert.
Artikel-Datei: Kugelstoss.pdf (287 K)
Eurotunnel
von Klaus Becker und Katrin Riepl
Die Streckenführung des Eurotunnels unter dem Ärmelkanal soll unter Berücksichtigung der geographischen und geologischen Gegebenheiten in vereinfachter Form durch verschiedene Funktiontypen, wie „ganzrational“, „stückweise linear“ oder „abwechselnd linear und kubisch“ nachkonstruiert werden. Dabei werden die Bedingungen zur Festlegung der Funktion mit Derive ausgewertet. Außerdem erlaubt Derive einen schnellen graphischen Vergleich der Graphen der Modellfunktion mit dem tatsächlichen Tunnelverlauf und damit eine direkte Bewertung der Modellierung.
Artikel-Datei: Eurotunnel.pdf (357 K)
Vom Modell zur Differentialgleichung
von Gregor Noll
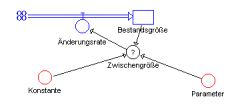
Nach der Modellierung mit einem graphischen Modellbildungsystem werden für verschiedene Beispiele aus den Modellgleichungen die dahinterliegenden Differentialgleichungen abgeleitet. Die Lösungen der Diffentialgleichungen werden mit dem TI92 graphisch über das Steigungsfeld und exakt mit Hilfe des CAS ermittelt und mit den Lösungen des Modellbildungssystems verglichen
Artikel-Datei: modelldgl.pps (370 K)
Ein Verkehrsproblem
von Benno Grabinger
Geinsheim liegt in der Pfalz, in der Mitte zwischen Neustadt und Speyer. Geinsheim ist ein Ortsteil von Neustadt an der Weinstraße.
Seit Jahren nimmt die Verkehrsbelastung in Geinsheim immer weiter zu. Die Ursache dafür ist die B39 die direkt durch die Hauptstraße von Geinsheim führt. Mittlerweile sind es 15.000 Autos und LKWs pro Tag die den Ort passieren. Dies führt zu massiven Lärmbelästigung der Anwohner, starken Abgasemissionen und zu einer hohen Unfallgefahr.
In dem Artikel wird die Trassenführung einer Ortsumgehung analysiert und mit Hilfe des TI92 bzw. Derive konstruiert.
Artikel-Archiv: geinsheim.zip (335 K)
